Kinh tế, tài chính > Chính trị, kinh tế, tài chính - Khác

Cách giải phương trình bậc 3?

Cách giải phương trình bậc 3 có bạn nào biết không, chỉ mình với.

An Khoi
An Khoi
Trả lời 9 năm trước

Cách giải phương trình bậc 3 theo phương phápCardano

Trước tiên, chia phương trình cho α3để đưa về dạng

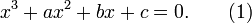
x^3 + ax^2 + bx +c = 0. qquad (1)

Đặtx=t-a/3 và biến đổi ta có phương trình

t^3 + pt + q = 0,trong đó p = b - frac{a^2}3vàq = c + frac{2a^3-9ab}{27}. qquad (2)

Nó được gọi là phương trình bậc basuy biến.

Ta sẽ tìm các sốuvàvsao cho

u^3-v^3 = q và uv = frac{p}{3}. qquad (3)

một nghiệm của nó tìm được từ việc đặt

t = v - u, ,

có thể kiểm tra trực tiếp khi thay giá trịtvào (2), nhờ hằng đảng thức lập phương của nhị thức

(v-u)^3+3uv(v-u)+(u^3-v^3)=0 ,

Hệ (3) có thể giải từ phương trình thứ hai rútv, ta có

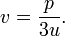
v = frac{p}{3u}.

Thay vào phương trình thứ nhất trong (3) ta có

u^3 - frac{p^3}{27u^3} = q.

Phương trình này tương đương với một phương trình bậc hai vớiu3. Khi giải, ta tìm được

u=sqrt[3]{{qover 2}pm sqrt{{q^{2}over 4}+{p^{3}over 27}}}. qquad (4)

Vìt=v−uvàt=x+a/3, ta tìm được

x=frac{p}{3u}-u-{aover 3}.

Chú ý rằng, có sáu giá trịutìm được từ (4), vì có hai căn bậc ba ứng với hai dấu (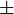pm), và mỗi căn bậc ba có ba giá trị (một giá trị thực và hai tích của nó với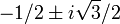-1/2 pm isqrt{3}/2). Tuy nhiên, dấu của các căn phải chọn sao cho khi tínhx, không gặp trường hợp chia cho không. Thứ nhất, nếup= 0, thì chọn dấu của căn bậc hai sao choukhác 0, i.e.u = sqrt[3]{q}. Thứ hai, nếup=q= 0, thì ta cóx= −a/3.

CÂU HỎI LIÊN QUAN